what are the solutions to the system of equations graphed below

Learning Outcomes

• Graph systems of equations
  • Graph a system of two linear equations
  • Graph a system of ii linear inequalities
• Evaluate ordered pairs as solutions to systems
  • Determine whether an ordered pair is a solution to a organisation of linear equations
  • Determine whether an ordered pair is a solution to a organisation of linear inequalities
• Classify solutions to systems
  • Identify what type of solution a system will have based on its graph

The way a river flows depends on many variables including how big the river is, how much water it contains, what sorts of things are floating in the river, whether or not it is raining, and and then forth. If y'all want to all-time describe its flow, you must take into business relationship these other variables. A organization of linear equations can help with that.

A system of linear equations consists of two or more linear equations made up of ii or more variables such that all equations in the organisation are considered simultaneously. You lot will notice systems of equations in every application of mathematics. They are a useful tool for discovering and describing how behaviors or processes are interrelated. It is rare to notice, for example, a pattern of traffic flow that that is but affected past weather. Accidents, time of day, and major sporting events are just a few of the other variables that tin bear on the menses of traffic in a city. In this section, we will explore some basic principles for graphing and describing the intersection of two lines that make upwards a organisation of equations.

Graph a system of linear equations

In this section, we volition wait at systems of linear equations and inequalities in ii variables.  First, we will exercise graphing two equations on the same set of axes, and so nosotros volition explore the unlike considerations you demand to brand when graphing two linear inequalities on the same prepare of axes. The aforementioned techniques are used to graph a system of linear equations as you lot take used to graph single linear equations. Nosotros can utilize tables of values, slope and y-intercept, or 10– and y-intercepts to graph both lines on the same fix of axes.

For example, consider the following system of linear equations in two variables.

[latex]\begin{array}{r}2x+y=-eight\\ 10-y=-1\stop{array}[/latex]

Allow'due south graph these using slope-intercept form on the same set of axes. Remember that slope-intercept form looks like [latex]y=mx+b[/latex],  and then we will desire to solve both equations for [latex]y[/latex].

Kickoff, solve for y in [latex]2x+y=-eight[/latex]

[latex]\begin{array}{c}2x+y=-eight\\ y=-2x - 8\cease{array}[/latex]

2d, solve for y in [latex]x-y=-1[/latex]

[latex]\begin{array}{r}x-y=-1\,\,\,\,\,\\ y=x+1\end{array}[/latex]

The system is now written every bit

[latex]\brainstorm{array}{c}y=-2x - viii\\y=x+one\stop{array}[/latex]

Now yous tin can graph both equations using their slopes and intercepts on the aforementioned set of axes, as seen in the figure below. Note how the graphs share one point in common. This is their point of intersection, a point that lies on both of the lines.  In the adjacent section we will verify that this signal is a solution to the arrangement.

 In the following example, y'all volition be given a system to graph that consists of two parallel lines.

Example

Graph the system [latex]\begin{assortment}{c}y=2x+1\\y=2x-3\end{assortment}[/latex] using the slopes and y-intercepts of the lines.

In the next instance, y'all volition be given a system whose equations look different, just after graphing, turn out to be the same line.

Example

Graph the system [latex]\begin{array}{c}y=\frac{1}{2}10+two\\2y-x=four\end{array}[/latex] using the ten – and y-intercepts.

Graphing a system of linear equations consists of choosing which graphing method you want to use and cartoon the graphs of both equations on the aforementioned set of axes. When you graph a system of linear inequalities on the same set of axes, there are a few more things you will demand to consider.

Graph a system of 2 inequalities

Call up from the module on graphing that the graph of a single linear inequality splits the coordinate plane into 2 regions. On one side lie all the solutions to the inequality. On the other side, there are no solutions. Consider the graph of the inequality [latex]y<2x+5[/latex].

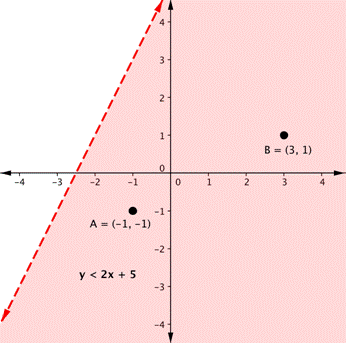
The dashed line is [latex]y=2x+5[/latex]. Every ordered pair in the shaded expanse below the line is a solution to [latex]y<2x+5[/latex], every bit all of the points below the line volition make the inequality true. If you lot doubt that, try substituting the x and y coordinates of Points A and B into the inequality—you'll see that they work. So, the shaded area shows all of the solutions for this inequality.

The boundary line divides the coordinate plane in half. In this case, it is shown as a dashed line as the points on the line don't satisfy the inequality. If the inequality had been [latex]y\leq2x+five[/latex], then the boundary line would have been solid.

Allow's graph another inequality: [latex]y>−x[/latex]. You can check a couple of points to determine which side of the boundary line to shade. Checking points M and N yield true statements. So, we shade the area in a higher place the line. The line is dashed as points on the line are not truthful.

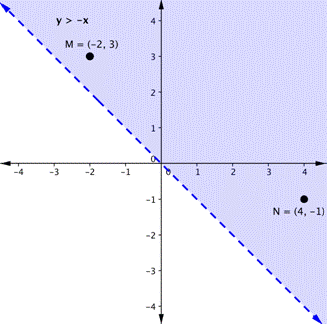
To create a system of inequalities, y'all demand to graph two or more than inequalities together. Permit'south use [latex]y<2x+5[/latex] and [latex]y>−ten[/latex] since we have already graphed each of them.

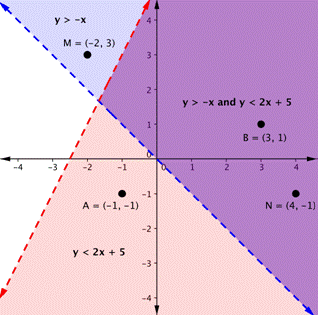
The purple area shows where the solutions of the two inequalities overlap. This expanse is the solution to the organisation of inequalities. Any signal within this purple region volition be true for both [latex]y>−10[/latex] and [latex]y<2x+5[/latex].

In the next example, you lot are given a system of two inequalities whose purlieus lines are parallel to each other.

Examples

Graph the organization [latex]\brainstorm{array}{c}y\ge2x+1\\y\lt2x-three\end{array}[/latex]

In the next section, we will run into that points can exist solutions to systems of equations and inequalities.  We volition verify algebraically whether a signal is a solution to a linear equation or inequality.

Determine whether an ordered pair is a solution for a arrangement of linear equations

The lines in the graph above are defined as

[latex]\begin{array}{r}2x+y=-8\\ ten-y=-1\end{array}[/latex].

They cross at what appears to be [latex]\left(-iii,-2\correct)[/latex].

Using algebra, we can verify that this shared signal is actually [latex]\left(-3,-2\right)[/latex] and not [latex]\left(-2.999,-1.999\right)[/latex]. Past substituting the x– and y-values of the ordered pair into the equation of each line, you lot can exam whether the indicate is on both lines. If the substitution results in a truthful statement, then you lot take constitute a solution to the organisation of equations!

Since the solution of the system must be a solution to all the equations in the organization, you volition need to check the point in each equation. In the following example, nosotros will substitute -3 for x and -2 for y in each equation to test whether it is actually the solution.

Example

Is [latex]\left(-3,-2\right)[/latex] a solution of the arrangement

[latex]\begin{array}{r}2x+y=-viii\\ x-y=-1\end{array}[/latex]

Example

Is (3, nine) a solution of the system

[latex]\brainstorm{array}{r}y=3x\\2x–y=6\finish{array}[/latex]

Recall Well-nigh Information technology

Is [latex](−ii,4)[/latex] a solution for the system

[latex]\begin{assortment}{r}y=2x\\3x+2y=1\end{assortment}[/latex]

Earlier you do any calculations, look at the point given and the beginning equation in the arrangement.  Can you lot predict the answer to the question without doing any algebra?

Remember that in society to be a solution to the system of equations, the values of the point must exist a solution for both equations. Once you discover 1 equation for which the point is imitation, you have determined that it is non a solution for the system.

We tin can employ the same method to make up one's mind whether a point is a solution to a organization of linear inequalities.

Make up one's mind whether an ordered pair is a solution to a arrangement of linear inequalities

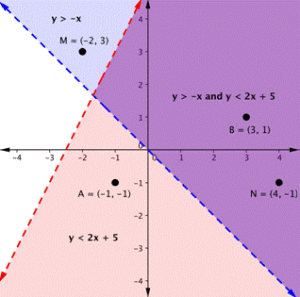
On the graph above, yous can see that the points B and Northward are solutions for the system because their coordinates will brand both inequalities true statements.

In contrast, points M and A both lie outside the solution region (majestic). While point Thou is a solution for the inequality [latex]y>−x[/latex] and point A is a solution for the inequality [latex]y<2x+5[/latex], neither betoken is a solution for the organization. The following example shows how to examination a point to see whether it is a solution to a system of inequalities.

Example

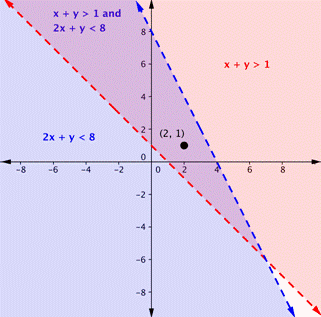
Is the indicate (2, 1) a solution of the system [latex]10+y>1[/latex] and [latex]2x+y<viii[/latex]?

Here is a graph of the system in the example above. Notice that (two, 1) lies in the purple surface area, which is the overlapping area for the two inequalities.

Instance

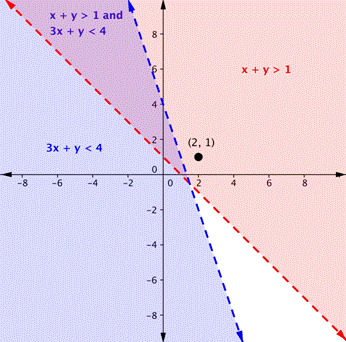
Is the signal (2, 1) a solution of the system [latex]x+y>1[/latex] and [latex]3x+y<4[/latex]?

Here is a graph of this system. Notice that (2, 1) is not in the purple area, which is the overlapping area; it is a solution for one inequality (the cherry-red region), but it is not a solution for the 2d inequality (the blueish region).

Every bit shown above, finding the solutions of a organization of inequalities can exist washed past graphing each inequality and identifying the region they share. Below, you are given more than examples that show the entire procedure of defining the region of solutions on a graph for a organisation of two linear inequalities.  The general steps are outlined below:

• Graph each inequality as a line and determine whether it will be solid or dashed
• Decide which side of each boundary line represents solutions to the inequality by testing a point on each side
• Shade the region that represents solutions for both inequalities

Example

Shade the region of the graph that represents solutions for both inequalities.  [latex]x+y\geq1[/latex] and [latex]y–x\geq5[/latex].

In this department we take seen that solutions to systems of linear equations and inequalities can exist ordered pairs. In the next section, we will piece of work with systems that have no solutions or infinitely many solutions.

Use a graph to classify solutions to systems

Recall that a linear equation graphs equally a line, which indicates that all of the points on the line are solutions to that linear equation. There are an infinite number of solutions. As we saw in the last department, if y'all have a system of linear equations that intersect at ane signal, this point is a solution to the system.  What happens if the lines never cross, as in the case of parallel lines?  How would you describe the solutions to that kind of system? In this section, nosotros will explore the three possible outcomes for solutions to a system of linear equations.

Three possible outcomes for solutions to systems of equations

Recall that the solution for a arrangement of equations is the value or values that are true for all equations in the organisation. There are three possible outcomes for solutions to systems of linear equations.  The graphs of equations within a arrangement can tell you lot how many solutions exist for that arrangement. Wait at the images below. Each shows two lines that brand up a system of equations.

One Solution	No Solutions	Infinite Solutions
If the graphs of the equations intersect, so there is one solution that is truthful for both equations.	If the graphs of the equations do not intersect (for example, if they are parallel), then at that place are no solutions that are true for both equations.	If the graphs of the equations are the aforementioned, then in that location are an infinite number of solutions that are true for both equations.

• 1 Solution: When a organization of equations intersects at an ordered pair, the organization has one solution.
• Infinite Solutions: Sometimes the 2 equations will graph every bit the same line, in which case we accept an infinite number of solutions.
• No Solution: When the lines that make up a organisation are parallel, there are no solutions because the two lines share no points in common.

Case

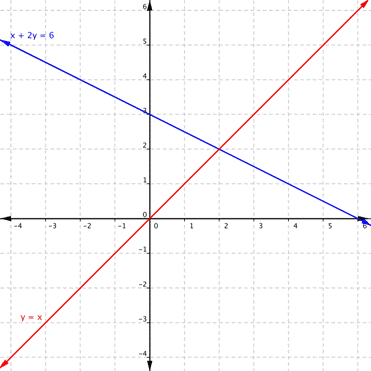
Using the graph of [latex]\brainstorm{assortment}{r}y=ten\\x+2y=6\end{array}[/latex], shown below, determine how many solutions the organisation has.

Instance (Advanced)

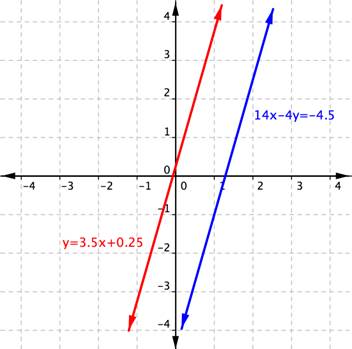
Using the graph of [latex]\begin{assortment}{r}y=three.5x+0.25\\14x–4y=-four.5\cease{array}[/latex], shown below, determine how many solutions the system has.

Example

How many solutions does the system [latex]\begin{array}{r}y=2x+1\\−4x+2y=2\end{array}[/latex] accept?

In the next department, we will learn some algebraic methods for finding solutions to systems of equations.  Recall that linear equations in ane variable tin can have one solution, no solution, or many solutions and we can verify this algebraically.  We will use the same ideas to classify solutions to systems in 2 variables algebraically.

hernandezkneand1992.blogspot.com

Source: https://courses.lumenlearning.com/beginalgebra/chapter/introduction-to-systems-of-linear-equations/

Share this post